算法思想

简述算法设计的10种通用技术

蛮力法

思想：蛮力法(brute force)是一种简单直接地解决问题的方法，常常直接基于问题的描述和所涉及的概念定义。

例子：对于给定的数字a和一个非负的整数n，计算aⁿ的值。可以简单地把1和a相乘n次来得到aⁿ的值。

应用：

• 排序：选择排序和冒泡排序
• 查找：排序查找和蛮力字符串匹配
• 穷举查找：旅行商问题、背包问题和分配问题
• 运筹学：最近对问题
• 计算几何：凸包问题
• 图论：深度优先查找和广度优先查找

减治法

思想：减治(decrease-and-conquer)技术利用了一个问题给定实例的解和同样问题较小实例的解之间的某种关系。一旦建立了这种关系，我们既可以从顶至下，也可以从底至上来运用该关系。

自底向上版本往往是迭代实现的，从求解问题的一个较少实例开始，该方法有时也称为增量法(Incremental Approach)

就是把问题分为子问题，把子问题都解决了，问题也就迎刃而解了。

减治法的流程

变化形式

• 减去一个常量（减一）
• 减去一个常量因子（减半）
• 减去的规模是可变的（ gcd(m,n) = gcd(n,m mod n) ）

应用

• 减一：插入排序（递归思想）和拓扑排序
• 减半：折半查找，假币问题，俄式算法，约瑟夫斯问题
• 减可变规模：选择问题，插值查找，二叉查找树的查找和插入，拈游戏

分治法

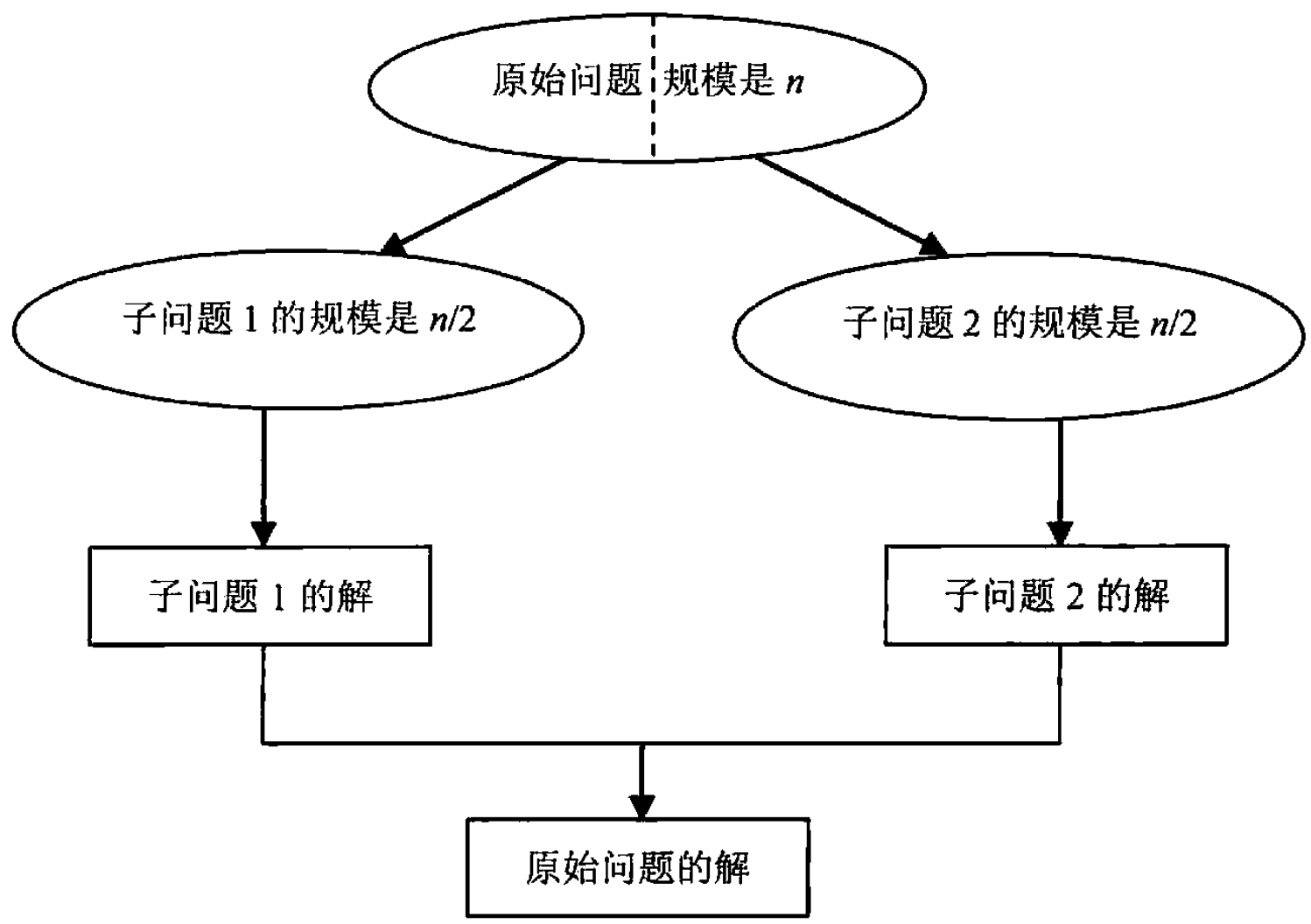
思想：分治法是一种一般性的算法设计技术，它将问题的实例划分为若干个较小的实例（最好拥有同样的规模），对这些较小的实例递归求解，然后合并这些解，以得到原始问题的解。

工作流程：

1. 将一个问题划分为同一类型的若干子问题，子问题最好规模相同。
2. 对这些子问题求解（一般使用递归方法，但在问题规模足够小时，有时也会利用另一个算法）。
3. 有必要的话，合并这些子问题的解，以得到原始问题的答案。

分治法的典型流程

应用

• 合并排序
• 快速排序
• 二叉树遍历
• 大整数乘法和 Strassen 矩阵乘法
• 最近对问题和凸包问题

变治法

思想：变治法(transform-and-conquer) ，在’变’的阶段，把问题的实例变得更容易求解。在’治’的阶段，对实例进行求解。

类型

• 实例化简(instance simplification)：变换为同样问题的一个更简单或更方便的实例
• 改变表现(representation change)：变换为同样实例的不同表现
• 问题化简(problem reduction)：变换为另一个问题的实例

例子：二元一次方程组的求解，先把一个变量表示为另一个变量的函数，再把这个结果代入另一个方程中，得到一个线性方程，然后用它的解来求出另一个变量的值。

应用

• 预排序
• 高斯消去法
• 平衡查找树
• 堆和堆排序
• 霍纳法则和二进制幂

时空权衡

空间换时间要比时间换空间普遍得多。

空间换时间的主要类型：

• 输入增强(input enhancement)，对问题的部分或全部输入做预处理，然后将获得的额外信息进行存储，以加速后面问题的求解。
• 动态规划(dynamic programming)，把给定问题中重复子问题的解记录在表中，然后求得所讨论问题的解。

例子：在函数定义域的多个点上计算函数值的问题。

如果运算时间更为重要的话，可以事先把函数值计算好并将它们存储在一张表中。

应用

• 计数法排序
• Boyer-Moore 字符串匹配算法
• 散列法
• B 树

动态规划

思想：动态规划(dynamic programming)，是一种使多阶段决策过程最优的通用方法。一般来说，这样的子问题出现在求解给定问题的递推关系中，这个递推关系中包含了相同类型的更小子问题的解。动态规划法建议，与其对交叠子问题一次又一次地求解，还不如对每个较小的子问题只解一次并把结果记录在表中，这样就可以从表中得出原始问题的解。

最优化法则(principle of optimality)，最优化问题任一实例的最优解，都是由其子实例的最优解构成的。

例子：求解最优化问题。

应用

• 币值最大化问题，找零问题，硬币收集问题
• 背包问题
• 最优二叉查找树
• Warshall 算法和Floyd 算法

贪心技术

思想：贪婪(greedy)法，通过一系列步骤来构造问题的解，每一步对目前构造的部分解做一个扩展，直到获得问题的完整解为止。

每一步都必须满足以下条件：

• 可行的(feasible)：必须满足问题的约束
• 局部最优(locally optimal)：当前步骤中所有可行选择中最佳的局部选择
• 不可取消(irrevocable)：选择一旦做出，在算法的后面步骤中就无法改变啦

每一步中，要求’贪婪’地选择最佳操作，并希望通过一系列局部的最优选择，能够产生一个整个问题的(全局的)最优解。

应用

• Prim 算法
• Kruskal 算法
• Dijkstra 算法
• 哈夫曼树及编码

迭代法

思想：迭代改进技术用来求最优问题的解，它生成一系列使问题的目标函数值不断改进的可行解。这一系列可行解中，后续解相比前面的解一般总是有些小的、局部的改变。如果目标函数值无法再得到优化，该算法就把最后的可行解作为最优解返回，然后算法就结束了。

应用

• 线性规划：单纯形法
• 最大流量问题：
• 二分图的最大匹配

回溯法

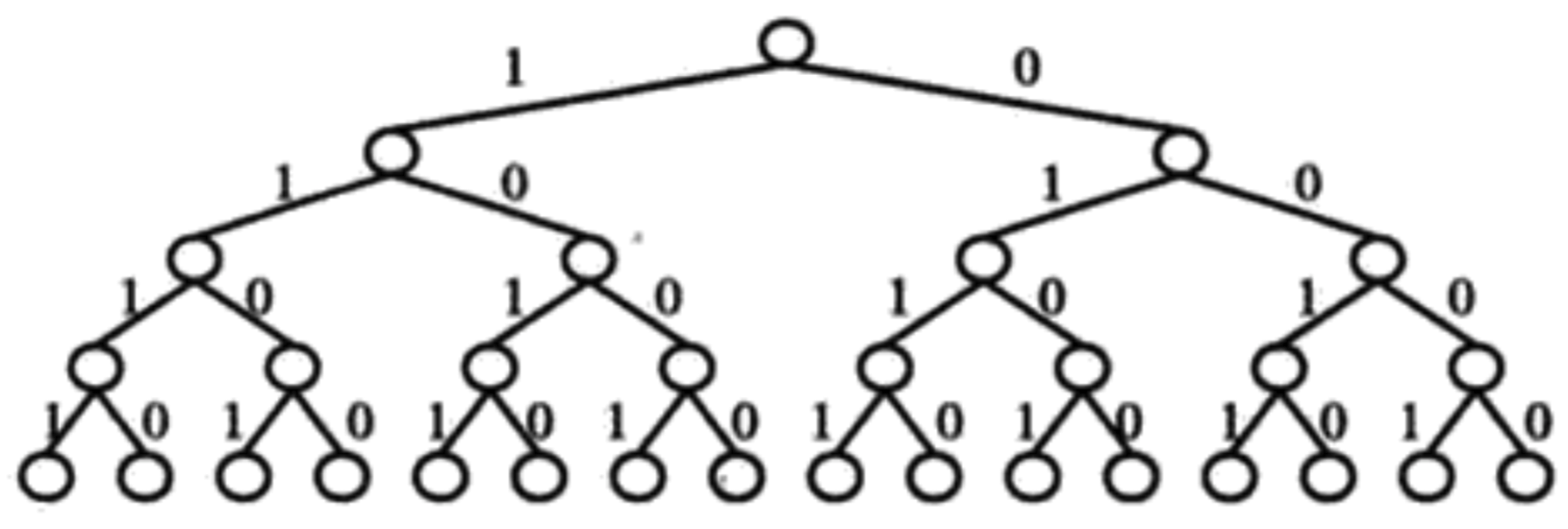
思想：在回溯法的大多数应用中，都按照深度优先查找法构造它的状态空间树。如果状态空间树的当前节点所代表的选择序列可以进一步扩展，而且不会违反问题的约束，它就会考虑下一个分量的第一个余下的合法选择。否则，这个方法就会回溯，也就是撤销部分构造解的最后一个分量，并用下一个选择来代替。

即一旦推导出无法从问题状态空间树的某个分支中产生一个解，我们就立即把这个分支砍掉。

状态空间树举例:

应用

• n 皇后问题
• 哈密顿回路问题

分支界限法

思想：只构造解的一个分量，一旦确定当前已经做出的选择无法导出一个解，就会立即终止当前步骤。

强化了状态空间树的生成方法。也就是估计可能从状态空间树的当前节点中求得的最佳值，如果这个估计值不超过当前过程中已经得到的最佳解，接下来就不会考虑该节点了。

应用

• 分配问题
• 背包问题
• 旅行商问题